Advaned Encryption Standard
AES is a symmetric encryption algorithm, which means it uses the same key for both encryption and decryption. It is used in many protocols, including TLS, which establishes a secure HTTP connection, also known as HTTPS. As you read this article, AES is probably protecting the data exchanged between this website and your device.
At its core, AES is an SP-network, operating on a 4×4 matrix of 16 bytes called the state.
The algorithm consists of multiple rounds. A round consists of four state transformations, with each step designed to provide confusion and diffusion properties that a good encryption algorithm usually has.
| AES Key Size | Rounds |
|---|---|
| 128-bit | 10 |
| 192-bit | 12 |
| 256-bit | 14 |
Let’s take a high-level overview of encryption and decryption, and then I will discuss each procedure in more detail.
Encryption
In short, the AES encryption process begins with key expansion; multiple round keys are derived from the main encryption key. After that, we simply perform rounds of operations: SubBytes, ShiftRows, MixColumns, and AddRoundKey.
Take a look at this diagram:
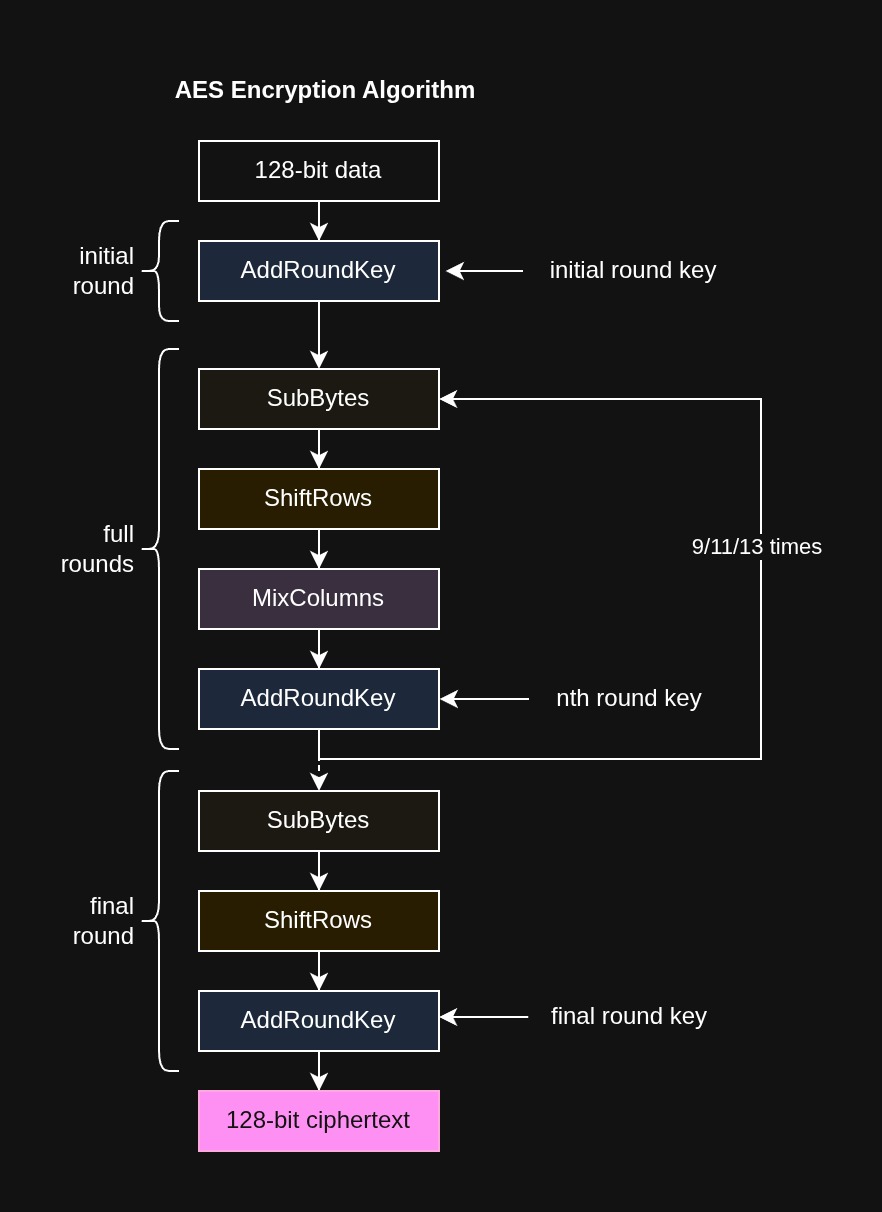
Decryption
For decryption we do almost the same, but in reverse order, using inverse versions of the operations: InvSubBytes, InvShiftRows, InvMixColumns, and AddRoundKey.
Also, note that in decryption, AddRoundKey comes before InvMixColumns to maintain mathematical properties.
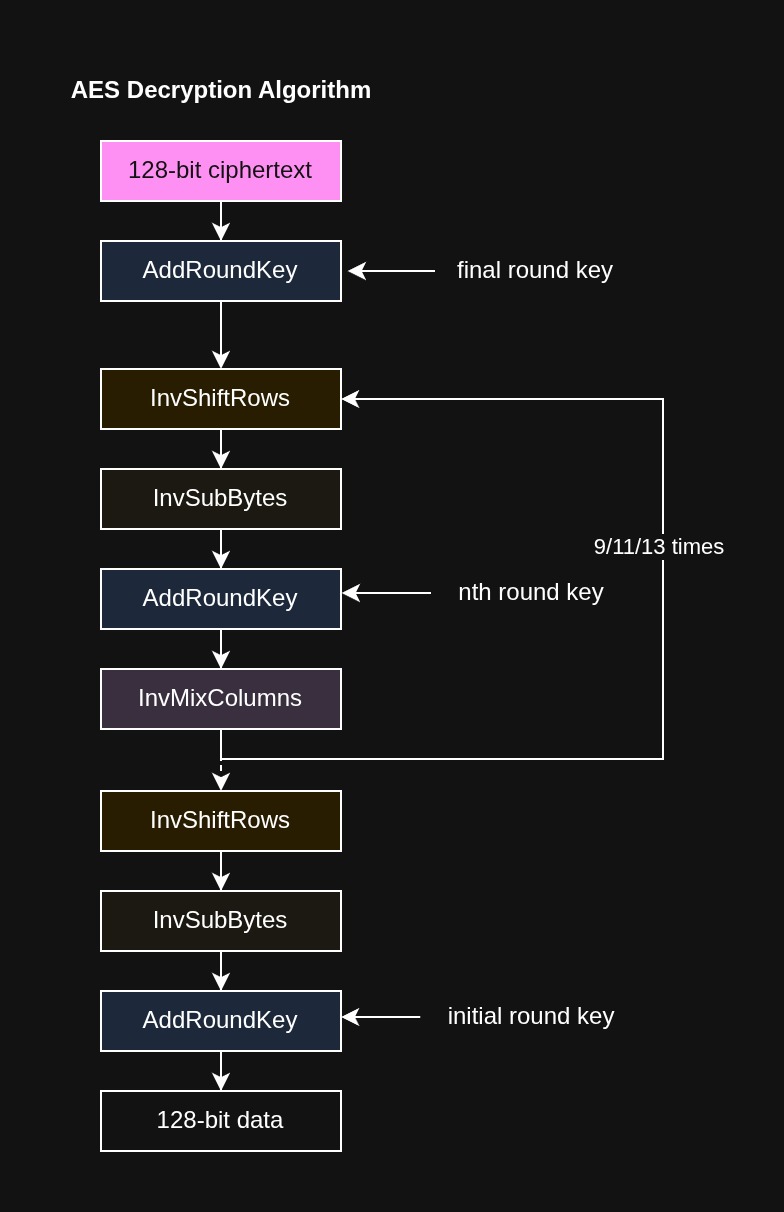
Let’s now look in more detail at each procedure.
Key Expansion
Before processing anything, we need round keys. They can be computed from the main encryption key using a specific algorithm called AES Key Schedule.
We will produce N+1 keys, where N is the number of main rounds. For example, in AES-256 we have 14 main rounds; we will generate 15 keys. One extra key is needed for the initial round.
We split our main key into words. In this context, a word is 4 bytes. So, one round key is 4 words, and its size is 16 bytes.
Initial words are just words of the main encryption key.
New words are computed through a combination of XOR operations with a previous word, depending on position, modified by special transformations.
When generating every Nth word (where N is the main key length in words), we rotate bytes one position left (RotWord), substitute them using sbox (SubWord), and the result is XORed with a round constant.
Round constants
| Round | Round Constant (RCON) |
|---|---|
| 1 | 0x01 |
| 2 | 0x02 |
| 3 | 0x04 |
| 4 | 0x08 |
| 5 | 0x10 |
| 6 | 0x20 |
| 7 | 0x40 |
| 8 | 0x80 |
| 9 | 0x1B |
| 10 | 0x36 |
| 11 | 0x6C |
| 12 | 0xD8 |
| 13 | 0xAB |
| 14 | 0x4D |
| 15 | 0x9A |
For AES-256, an additional SubWord operation occurs halfway through each expansion cycle.
We compute words until all round keys are completed.
Below are visual explanations of how the key schedule works for each key size. Sometimes it’s easier to explain using images than words.
AES-128 Key Expansion
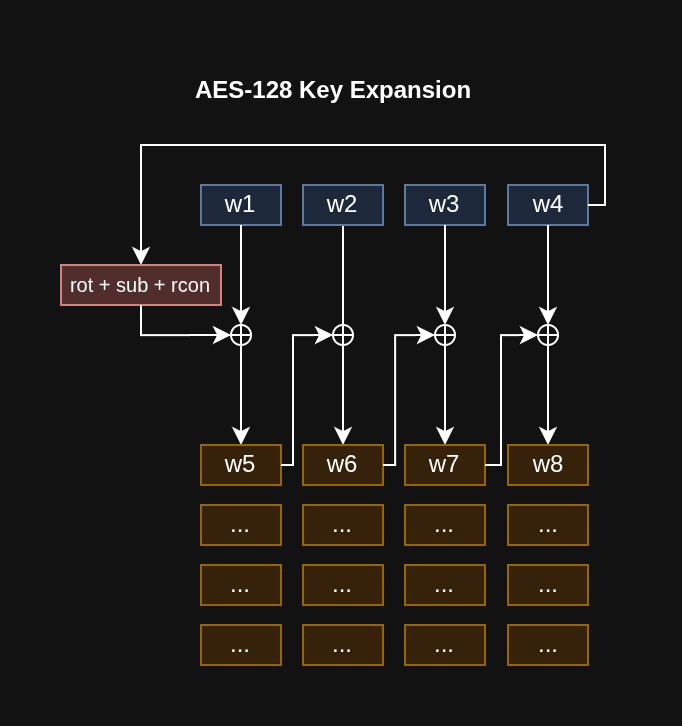
AES-192 Key Expansion
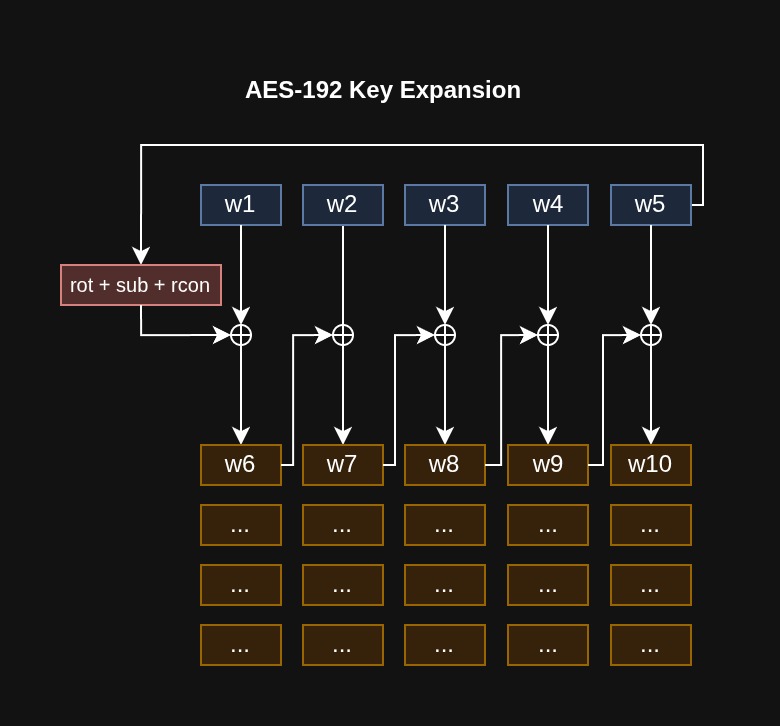
AES-256 Key Expansion
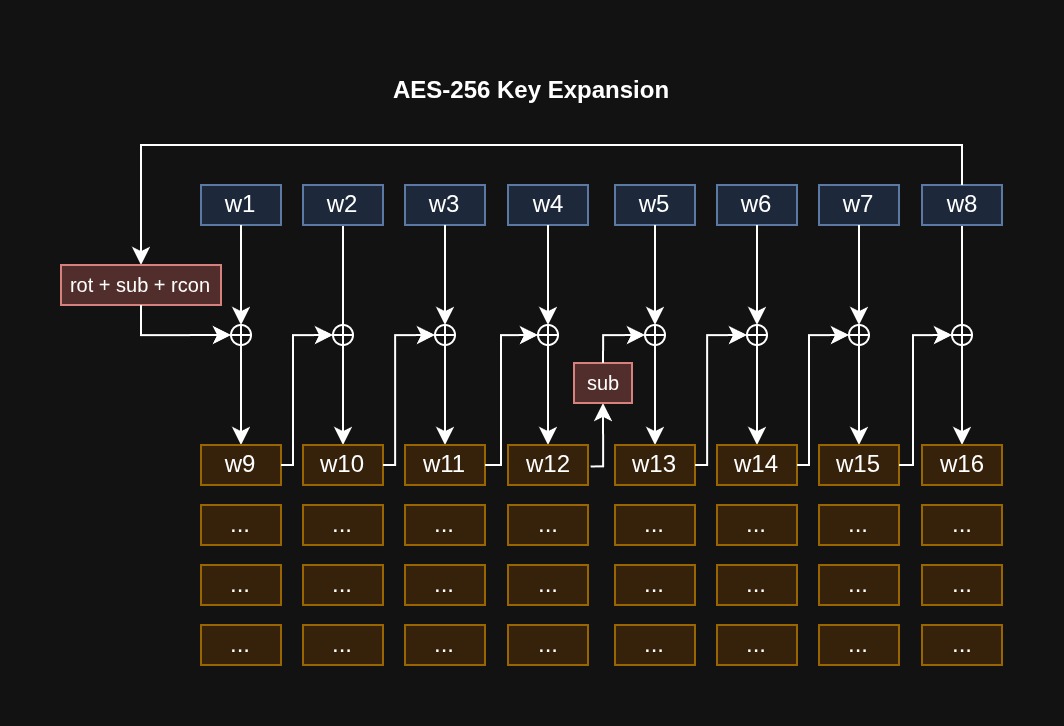
Once the key is expanded, we can go through core transformations starting with the SubBytes.
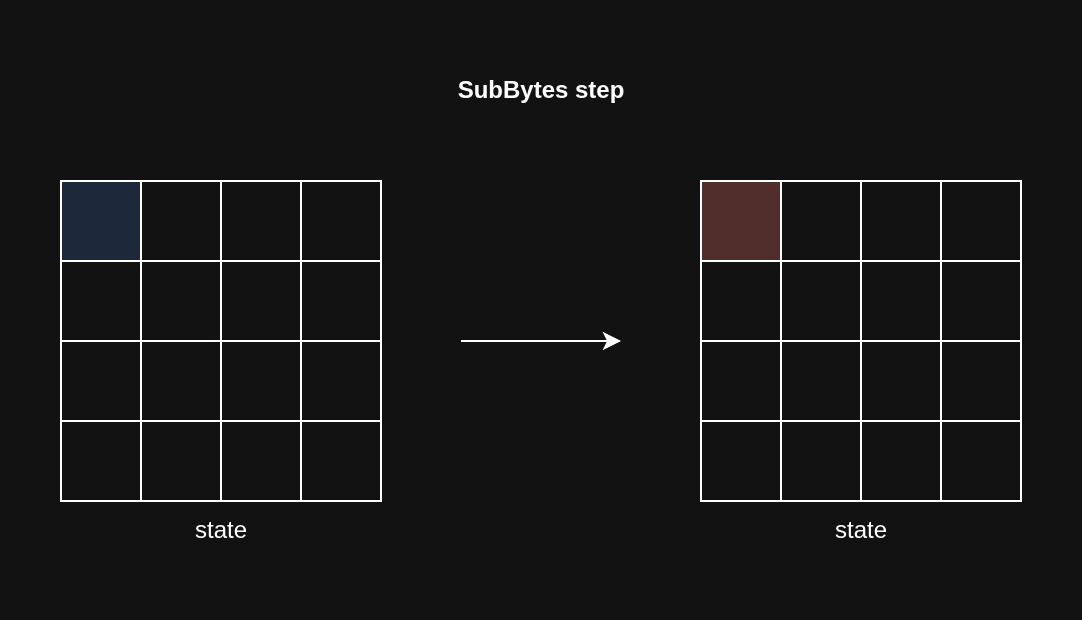
SubBytes
This is a non-linear substitution step where each byte is replaced with another according to a predetermined lookup table called the S-box.
The S-box table has 256 unique values. These are all possible values a single byte can have.
S-box table
| Byte | Replacer |
|---|---|
| 00000000 | 01100011 |
| 00000001 | 01111100 |
| 00000010 | 01110111 |
| 00000011 | 01111011 |
| 00000100 | 11110010 |
| 00000101 | 01101011 |
| 00000110 | 01101111 |
| 00000111 | 11000101 |
| 00001000 | 00110000 |
| 00001001 | 00000001 |
| 00001010 | 01100111 |
| 00001011 | 00101011 |
| 00001100 | 11111110 |
| 00001101 | 11010111 |
| 00001110 | 10101011 |
| 00001111 | 01110110 |
| 00010000 | 11001010 |
| 00010001 | 10000010 |
| 00010010 | 11001001 |
| 00010011 | 01111101 |
| 00010100 | 11111010 |
| 00010101 | 01011001 |
| 00010110 | 01000111 |
| 00010111 | 11110000 |
| 00011000 | 10101101 |
| 00011001 | 11010100 |
| 00011010 | 10100010 |
| 00011011 | 10101111 |
| 00011100 | 10011100 |
| 00011101 | 10100100 |
| 00011110 | 01110010 |
| 00011111 | 11000000 |
| 00100000 | 10110111 |
| 00100001 | 11111101 |
| 00100010 | 10010011 |
| 00100011 | 00100110 |
| 00100100 | 00110110 |
| 00100101 | 00111111 |
| 00100110 | 11110111 |
| 00100111 | 11001100 |
| 00101000 | 00110100 |
| 00101001 | 10100101 |
| 00101010 | 11100101 |
| 00101011 | 11110001 |
| 00101100 | 01110001 |
| 00101101 | 11011000 |
| 00101110 | 00110001 |
| 00101111 | 00010101 |
| 00110000 | 00000100 |
| 00110001 | 11000111 |
| 00110010 | 00100011 |
| 00110011 | 11000011 |
| 00110100 | 00011000 |
| 00110101 | 10010110 |
| 00110110 | 00000101 |
| 00110111 | 10011010 |
| 00111000 | 00000111 |
| 00111001 | 00010010 |
| 00111010 | 10000000 |
| 00111011 | 11100010 |
| 00111100 | 11101011 |
| 00111101 | 00100111 |
| 00111110 | 10110010 |
| 00111111 | 01110101 |
| 01000000 | 00001001 |
| 01000001 | 10000011 |
| 01000010 | 00101100 |
| 01000011 | 00011010 |
| 01000100 | 00011011 |
| 01000101 | 01101110 |
| 01000110 | 01011010 |
| 01000111 | 10100000 |
| 01001000 | 01010010 |
| 01001001 | 00111011 |
| 01001010 | 11010110 |
| 01001011 | 10110011 |
| 01001100 | 00101001 |
| 01001101 | 11100011 |
| 01001110 | 00101111 |
| 01001111 | 10000100 |
| 01010000 | 01010011 |
| 01010001 | 11010001 |
| 01010010 | 00000000 |
| 01010011 | 11101101 |
| 01010100 | 00100000 |
| 01010101 | 11111100 |
| 01010110 | 10110001 |
| 01010111 | 01011011 |
| 01011000 | 01101010 |
| 01011001 | 11001011 |
| 01011010 | 10111110 |
| 01011011 | 00111001 |
| 01011100 | 01001010 |
| 01011101 | 01001100 |
| 01011110 | 01011000 |
| 01011111 | 11001111 |
| 01100000 | 11010000 |
| 01100001 | 11101111 |
| 01100010 | 10101010 |
| 01100011 | 11111011 |
| 01100100 | 01000011 |
| 01100101 | 01001101 |
| 01100110 | 00110011 |
| 01100111 | 10000101 |
| 01101000 | 01000101 |
| 01101001 | 11111001 |
| 01101010 | 00000010 |
| 01101011 | 01111111 |
| 01101100 | 01010000 |
| 01101101 | 00111100 |
| 01101110 | 10011111 |
| 01101111 | 10101000 |
| 01110000 | 01010001 |
| 01110001 | 10100011 |
| 01110010 | 01000000 |
| 01110011 | 10001111 |
| 01110100 | 10010010 |
| 01110101 | 10011101 |
| 01110110 | 00111000 |
| 01110111 | 11110101 |
| 01111000 | 10111100 |
| 01111001 | 10110110 |
| 01111010 | 11011010 |
| 01111011 | 00100001 |
| 01111100 | 00010000 |
| 01111101 | 11111111 |
| 01111110 | 11110011 |
| 01111111 | 11010010 |
| 10000000 | 11001101 |
| 10000001 | 00001100 |
| 10000010 | 00010011 |
| 10000011 | 11101100 |
| 10000100 | 01011111 |
| 10000101 | 10010111 |
| 10000110 | 01000100 |
| 10000111 | 00010111 |
| 10001000 | 11000100 |
| 10001001 | 10100111 |
| 10001010 | 01111110 |
| 10001011 | 00111101 |
| 10001100 | 01100100 |
| 10001101 | 01011101 |
| 10001110 | 00011001 |
| 10001111 | 01110011 |
| 10010000 | 01100000 |
| 10010001 | 10000001 |
| 10010010 | 01001111 |
| 10010011 | 11011100 |
| 10010100 | 00100010 |
| 10010101 | 00101010 |
| 10010110 | 10010000 |
| 10010111 | 10001000 |
| 10011000 | 01000110 |
| 10011001 | 11101110 |
| 10011010 | 10111000 |
| 10011011 | 00010100 |
| 10011100 | 11011110 |
| 10011101 | 01011110 |
| 10011110 | 00001011 |
| 10011111 | 11011011 |
| 10100000 | 11100000 |
| 10100001 | 00110010 |
| 10100010 | 00111010 |
| 10100011 | 00001010 |
| 10100100 | 01001001 |
| 10100101 | 00000110 |
| 10100110 | 00100100 |
| 10100111 | 01011100 |
| 10101000 | 11000010 |
| 10101001 | 11010011 |
| 10101010 | 10101100 |
| 10101011 | 01100010 |
| 10101100 | 10010001 |
| 10101101 | 10010101 |
| 10101110 | 11100100 |
| 10101111 | 01111001 |
| 10110000 | 11100111 |
| 10110001 | 11001000 |
| 10110010 | 00110111 |
| 10110011 | 01101101 |
| 10110100 | 10001101 |
| 10110101 | 11010101 |
| 10110110 | 01001110 |
| 10110111 | 10101001 |
| 10111000 | 01101100 |
| 10111001 | 01010110 |
| 10111010 | 11110100 |
| 10111011 | 11101010 |
| 10111100 | 01100101 |
| 10111101 | 01111010 |
| 10111110 | 10101110 |
| 10111111 | 00001000 |
| 11000000 | 10111010 |
| 11000001 | 01111000 |
| 11000010 | 00100101 |
| 11000011 | 00101110 |
| 11000100 | 00011100 |
| 11000101 | 10100110 |
| 11000110 | 10110100 |
| 11000111 | 11000110 |
| 11001000 | 11101000 |
| 11001001 | 11011101 |
| 11001010 | 01110100 |
| 11001011 | 00011111 |
| 11001100 | 01001011 |
| 11001101 | 10111101 |
| 11001110 | 10001011 |
| 11001111 | 10001010 |
| 11010000 | 01110000 |
| 11010001 | 00111110 |
| 11010010 | 10110101 |
| 11010011 | 01100110 |
| 11010100 | 01001000 |
| 11010101 | 00000011 |
| 11010110 | 11110110 |
| 11010111 | 00001110 |
| 11011000 | 01100001 |
| 11011001 | 00110101 |
| 11011010 | 01010111 |
| 11011011 | 10111001 |
| 11011100 | 10000110 |
| 11011101 | 11000001 |
| 11011110 | 00011101 |
| 11011111 | 10011110 |
| 11100000 | 11100001 |
| 11100001 | 11111000 |
| 11100010 | 10011000 |
| 11100011 | 00010001 |
| 11100100 | 01101001 |
| 11100101 | 11011001 |
| 11100110 | 10001110 |
| 11100111 | 10010100 |
| 11101000 | 10011011 |
| 11101001 | 00011110 |
| 11101010 | 10000111 |
| 11101011 | 11101001 |
| 11101100 | 11001110 |
| 11101101 | 01010101 |
| 11101110 | 00101000 |
| 11101111 | 11011111 |
| 11110000 | 10001100 |
| 11110001 | 10100001 |
| 11110010 | 10001001 |
| 11110011 | 00001101 |
| 11110100 | 10111111 |
| 11110101 | 11100110 |
| 11110110 | 01000010 |
| 11110111 | 01101000 |
| 11111000 | 01000001 |
| 11111001 | 10011001 |
| 11111010 | 00101101 |
| 11111011 | 00001111 |
| 11111100 | 10110000 |
| 11111101 | 01010100 |
| 11111110 | 10111011 |
| 11111111 | 00010110 |
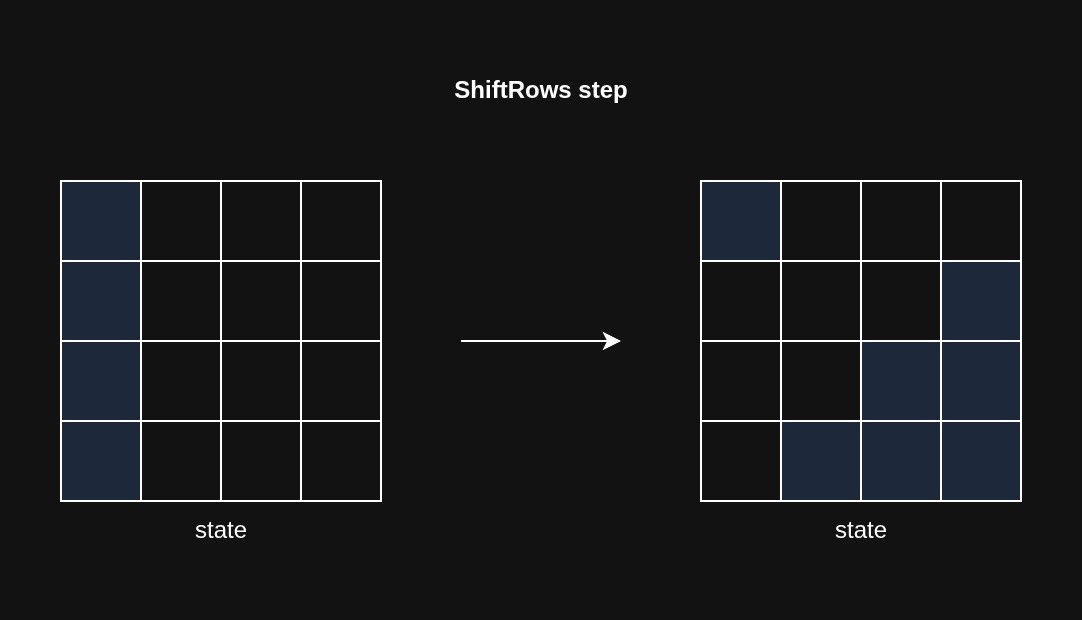
ShiftRows
In the ShiftRows step, each row does a cyclic left shift:
- R1: stays in place
- R2: moves 1 byte left
- R3: moves 2 bytes left
- R4: moves 3 bytes left
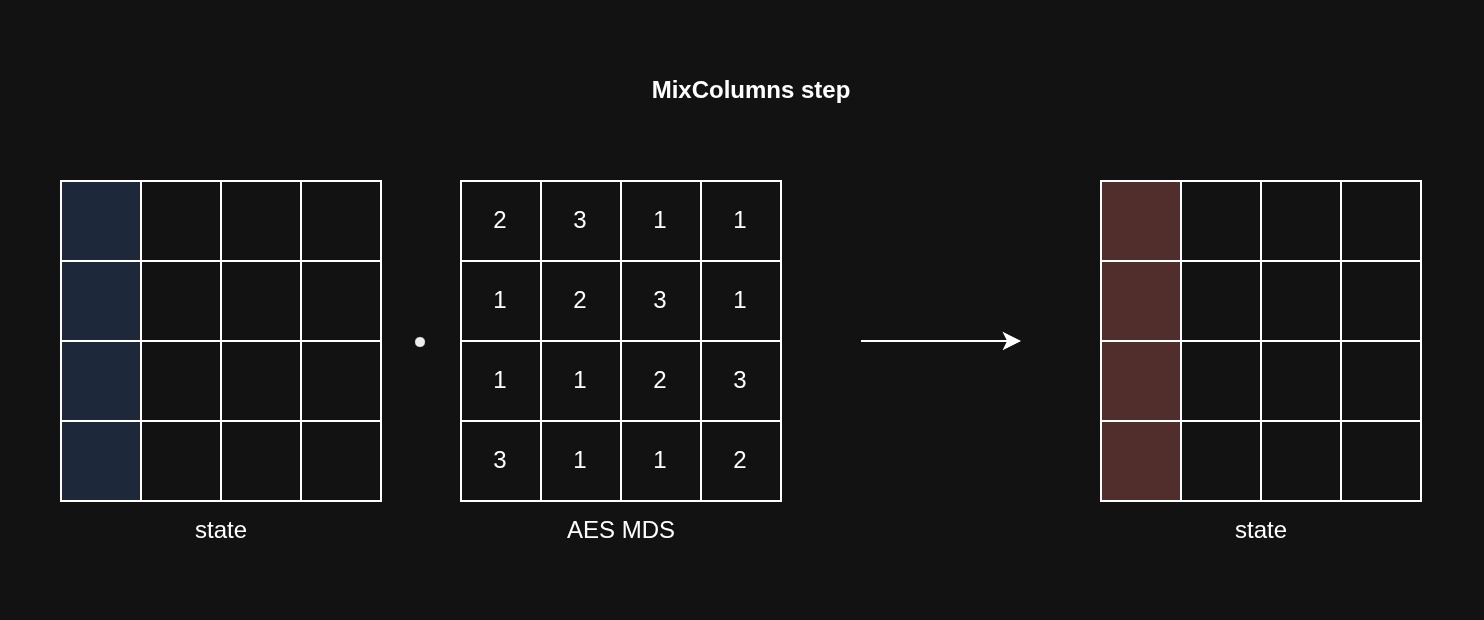
MixColumns
In the MixColumns step, each column is multiplied with a fixed 4x4 matrix over the Galois Field GF(2⁸).
This multiplication is not a standard dot product, but it’s a similar idea.
We represent each byte as a polynomial like this:
b7·x^7 + b6·x^6 + b5·x^5 + b4·x^4 + b3·x^3 + b2·x^2 + b1·x + b0
The “addition” during the matrix multiplication is performed using bitwise XOR, and the “multiplication” involves polynomial multiplication followed by a modular reduction using the irreducible polynomial x⁸+x⁴+x³+x+1.
This operation implements diffusion, where each cell depends on all other cells in the same column, making ciphertext hard to analyze.
Note: In the final round, we skip the MixColumn step to make decryption easier and also avoid extra computations.
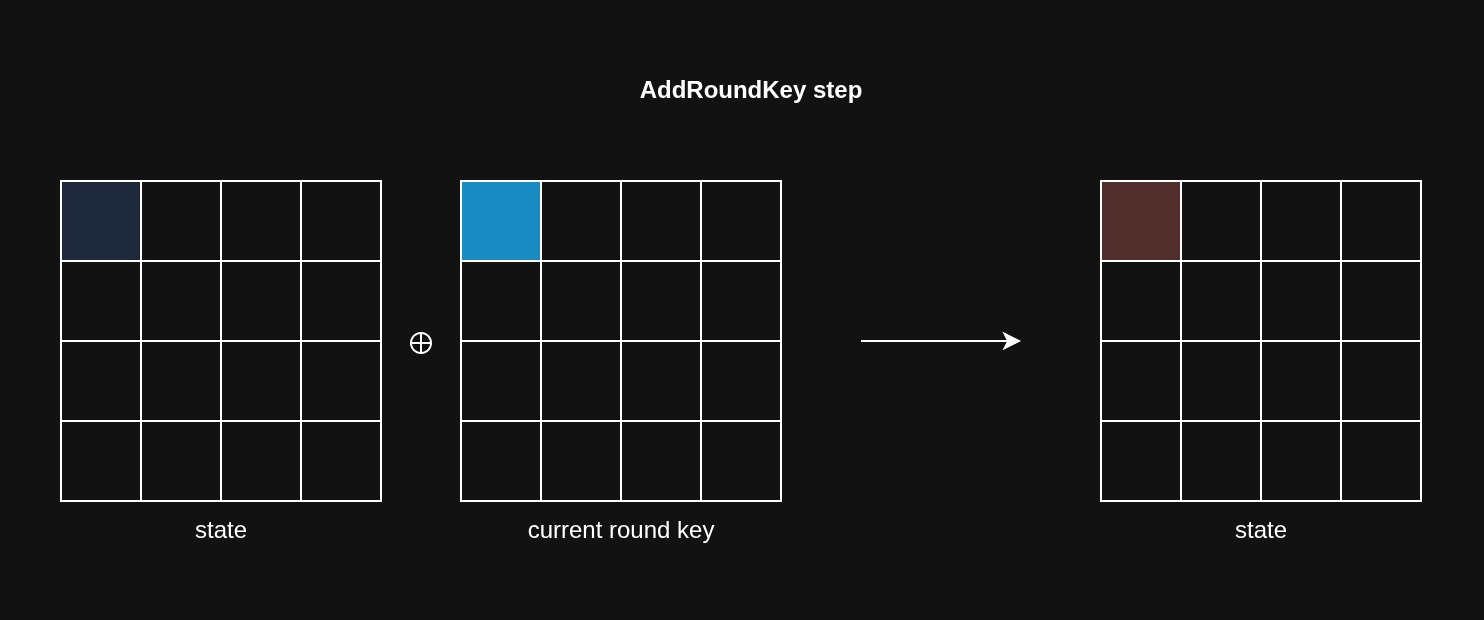
AddRoundKey
In this step, each byte of the state is matrix combined with the corresponding byte of the round key using the XOR operation.
By the way, there’s no need for a separate InvAddRoundKey step for decryption because applying the second XOR undoes the first one.
Operation Modes
To encrypt data larger than a single block, modes of operation, such as ECB, CBC, CTR, and GCM, are used. These modes determine how to securely apply encryption repeatedly across multiple blocks.
| Name | Abbrevation | Description |
|---|---|---|
| Electronic Codebook | ECB | Encrypts each block independently. |
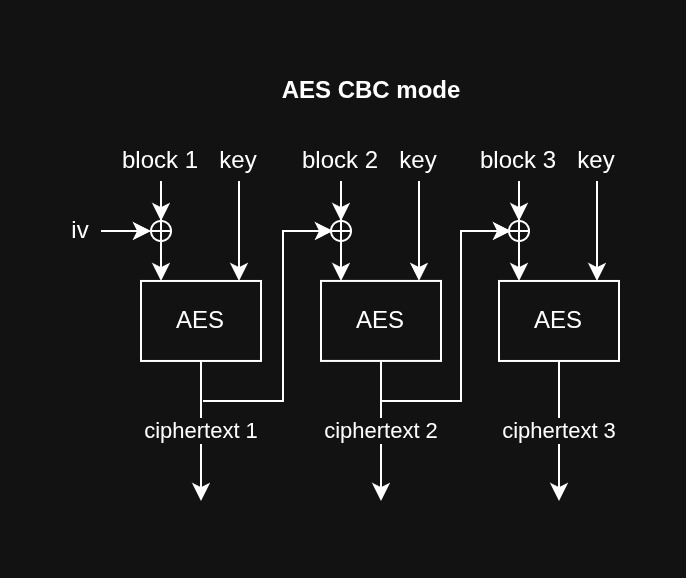
| Cipher Block Chaining | CBC | Each block is mixed with previous ciphertext. |
| Counter | CTR | Encrypts a counter value and mixes with a block. |
| Galois/Counter Mode | GCM | Combines CTR mode with integrity validation. |
Here’s a visual example of CBC mode:
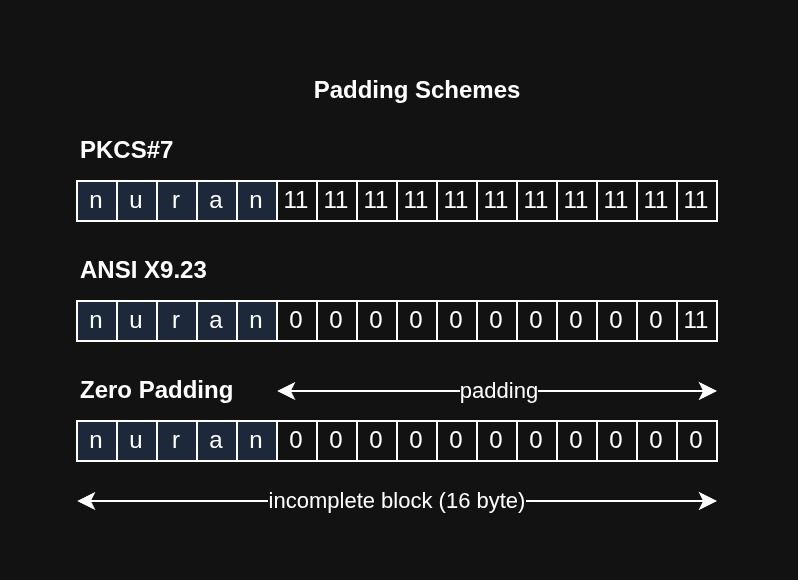
Padding Schemes
Plaintext isn’t always an exact multiple of AES’s block size, which is 16 bytes. To fill the remaining space, padding schemes are used. The well-known padding schemes are PKCS#7, ANSI X.923, and zero padding.
PKCS#7 adds N bytes of value N to complete a block. It always pads, even when data perfectly fits in 16 bytes, adding an extra full padding block.
ANSI X.923 sets the last padding byte to the length of padding and fills the rest with zeros. It also adds an additional padding block if no padding is needed.
Zero padding simply fills the empty space with zeros, though this can cause issues if the plaintext naturally ends with zeros.
Performance
AES was chosen as a standard not just because it performs good encryption, but also because it does it very fast.
Intel and AMD have even implemented direct CPU instructions for AES encryption.
Also, instead of performing polynomial multiplication in the MixColumns step on the fly, the results for all possible byte values can be precalculated and stored in lookup tables. Lookup table access time is usually O(1), which is constant time.
Thank you for reading this article about Advanced Encryption Standard. Have a good day!
You can check out the full AES-256-CBC implementation written by me in the C language in this repository.